Black-Scholesův model oceňování opcí
Black Scholesův model (BSM) je jeden z nejdůležitějších konceptů v moderní finanční teorii. Na jeho vývoji se podílela trojce mužů. Mr. Black, Mr. Scholes a Mr. Merton.
Jde vlastně o matematickou diferenciální rovnici, která odhaduje teoretickou hodnotu derivátů jiných investičních nástrojů. Tuto rovnici sestavili už v roce 1973 a stále je považována za nejlepší pro stanovení ceny opce.
Prvně dva zmínění pánové poprvé tuto rovnici publikovali v dokumentu The Pricing of Options and Corporate Liabilities. Tento dokument pomohl upravit pan Merton a později publikoval i své poznání s názvem Theory of Rational Option Pricing. V tomto svém poznání rozšířil matematické chápání a aplikaci již vytvořeného modelu pana Blacka a Scholese. Merton pak vytvořil právě termín, pojem – „Black-Scholesova teorie oceňování opcí“.
V roce 1997 dostal pan Merton a pan Scholes Nobelovu cenu za ekonomii. Bohužel ji nedostal pan Black. O dva roky dříve zemřel.
Vraťme se ale k samotnému modelu. Rovnici.
Předpokládá se, že cena podkladového aktiva se vyvíjí jako stochastický process. To znamená, že cena podkladového aktiva v čase t1, je nezávislá na ceně podkladového aktiva v čase t0.
Diferenciální rovnice má pět vstupních proměnných. Realizační cenu opce, aktuální cenu podkladového aktiva, dobu do expirace opčního kontraktu, bezrizikovou úrokovou sazbu a očekávanou volatilitu.
Standardní BSM se používá pouze k oceňování evropských opcí, protože nebere v úvahu, že by opční kontrakty mohly být uplatněny před datem expirace[1].
BSM je rychlý při výpočtu libovolného počtu opčních cen.
Black a Scholes stanovili určité předpoklady. Například, že během trvání opce nejsou vypláceny dividendy. Že pohyby na trhu nelze předvídat. Že nákup opce nemá transakční náklady. Že bezriziková úroková sazba a volatilita podkladového aktiva je známá a konstantní. Že výnos podkladového aktiva je logaritmicko-normálně rozdělen. Že opce je evropského typu.
Jelikož Black-Scholesův model nezohledňoval účinky dividend na cenu opce a také možné uplatnění opce před vypršením platnosti, začaly se objevovat různé modifikace tohoto oceňovacího modelu.
Na závěr si tedy ukažme, jak ta rovnice vypadá. Zdá se, že je to složité. Ale já to tu opravdu uvadím jen pro zajímavost. Nikdy to nebudeš potřebovat znát a nikdo Tě z toho zkoušet nebude. Takže si to rozhodně nemusíš pamatovat a nemusíš to ani pochopit.
Cena call opce podle Black-Scholesova vzorce se vypočítá vynásobením ceny podkladového aktiva kumulativní standardní funkcí normálního rozdělení pravděpodobnosti. Poté se od výsledné hodnoty z předchozího výpočtu odečte čistá současná hodnota realizační ceny vynásobená kumulativním standardním normálním rozdělením.
Zápis rovnice pro výpočet ceny call opce vypadá takto:
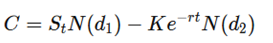
, kde:

a
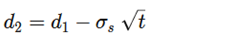
, kde:
C je výsledná cena call opce
S aktuální cena podkladového aktiva
K je realizační cena opce
r je bezriziková úroková sazba
t je čas do expirace
sigma je očekáváná volatilita
N normální rozdělení
Hmm, tak jo. Asi tak. Rozumíš tomu?
[1] Pro oceňování opcí amerického typu se používá binomický, nebo trinomický model, nebo také Bjerksund-Stenslandův model.
***
Tento článek je vyňat z knihy Chceš pochopit opce?, kterou jsem napsal na žádost několika z vás. Pokud si ji chceš celou přečíst už dnes, stáhni si celou knihu ZDARMA kliknutím na její obálku níže.↓

***
Máš jakýkoliv dotaz na svého brokera, nebo chceš pomoci se založením účtu? Přidej se do skupiny na Facebooku:
Interactive Brokers - https://www.facebook.com/groups/3066081436968059
DeGiro - https://www.facebook.com/groups/470168704825464
Trading 212 - https://www.facebook.com/groups/461483392253639
XTB - https://www.facebook.com/groups/242466764682430
Fio e-Broker - https://www.facebook.com/groups/668095940870592
LYNX Broker - https://www.facebook.com/groups/302071071962948
TastyTrade - https://www.facebook.com/groups/1683787365479097***
Chceš diskutovat s ostatními o tvých investičních plánech nebo nám něco sdělit? Přidej se sem: Akcie, Finanční trhy, Investice - Nová skupina od 31.12.2022 - https://www.facebook.com/groups/717903706577998***
Pokud rád čteš mé příspěvky a komentáře k tématu burzy, dej si „do lajku“ facebookovou stránku Investování pro všechny. Tak Ti neunikne ani jeden článek ode mne. Děkuji pěkně.